
Since their product is a square, both must be squares.
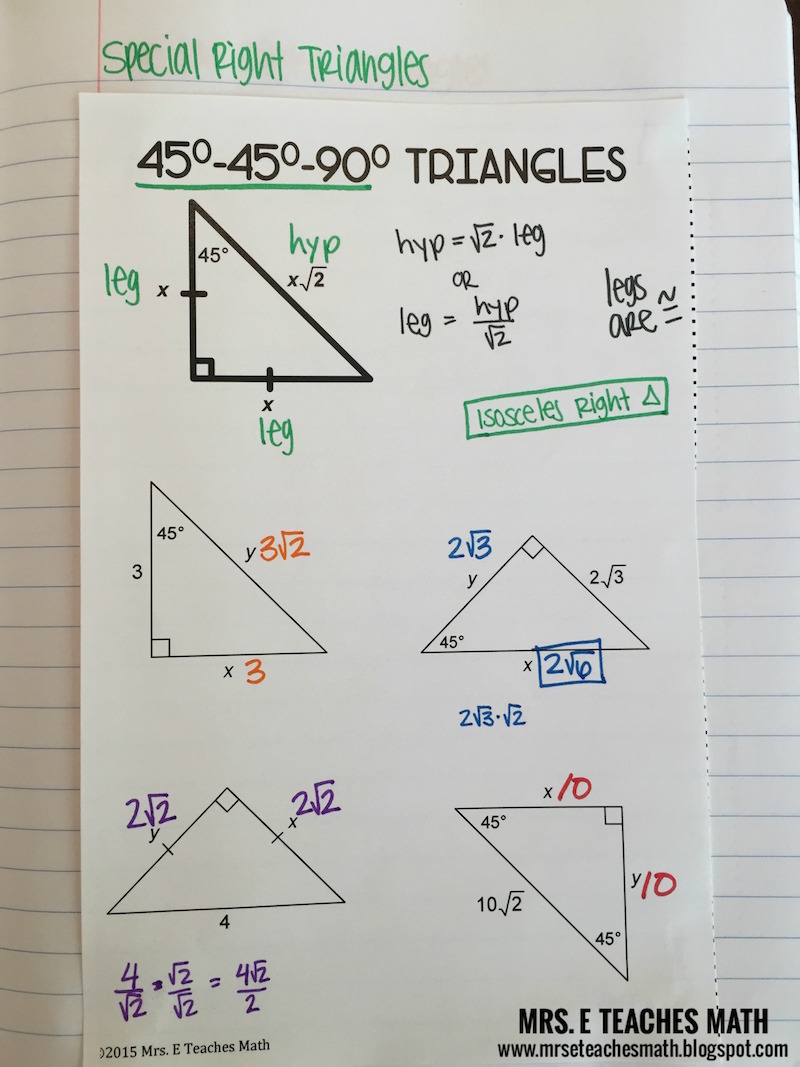
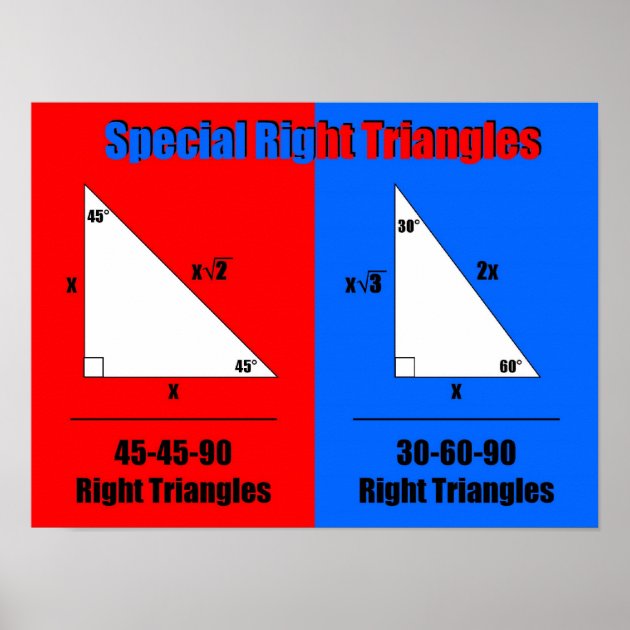
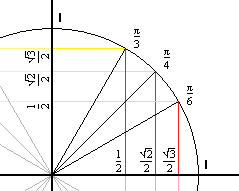
Then $p$ divides the sum, which is $c$, and the difference, which is $a$: absurd. Let $p$ be a prime dividing both $(c+a)/2$ and $(c-a)/2$. Items may require the use of the Pythagorean Theorem, special right triangles. This is impossible, because $c$ must be even, so $c=2C$ and we'd getĪssume, without loss of generality, that $a$ is odd and $b$ is even. If they were both odd, we could write $a=2A+1$ and $b=2B+1$, so A right triangle is a triangle which has a right angle (an angle of 90° or /2 radians). They can't be both even, because they are coprime. Answer: QUESTION: What is the difference between a right triangle and other triangles ANSWER: A triangle is a two dimensional geometric shape with three straight sides. One is the right triangle formed when an altitude is drawn from a vertex of an equilateral triangle, forming two congruent right triangles. There are two types of right triangles that every mathematician should know very well. Next we can show that $a$ and $b$ are of different parity: one is odd and the other is even. Figure : A right triangle The triangle above has side c as its hypotenuse, sides a and b as its legs, and angle C as its right angle. Thus we can assume that $a$ and $b$ are coprime, by factoring out all prime common divisors. Similarly, if $a$ and $c$ have a common prime divisor, this prime divides also $b$. G.2.5: Explain and use angle and side relationships in problems with special right triangles, such as 30, 60. If $p$ is a prime common divisor of $a$ and $b$, then $p$ also divides $c$: if $a=pA$ and $b=pB$, then $c^2=p^2(A^2+B^2)$, so that $p$ divides $c^2$, hence $c$.
Let $a,b,c$ be positive integers such that $a^2+b^2=c^2$.


 0 kommentar(er)
0 kommentar(er)
